CRYSTAL SYSTEMS AND BRAVAIS LATTICES
Crystal system is a method of classifying crystalline substances on the basis of their unit cell. There are seven unique crystal systems. The simplest and most symmetric, the cubic (or isometric) system, has the symmetry of a cube. The other six systems, in order of decreasing symmetry, are hexagonal, tetragonal, trigonal (also known as rhombohedral), orthorhombic, monoclinic and triclinic.
Bravais lattice is a set of points constructed by translating a single point in discrete steps by a set of basis vectors. In 1848, the French physicist and crystallographer Auguste Bravais (1811-1863) established that in three-dimensional space only fourteen different lattices may be constructed. All crystalline materials recognised till now fit in one of these arrangements.
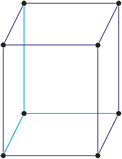
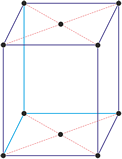
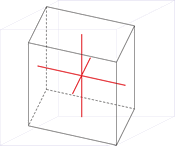
Cubic crystal system
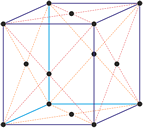
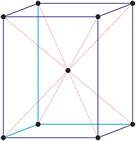
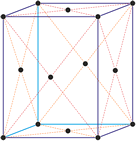
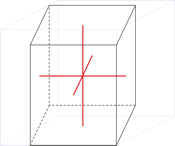
Cubic (or isometric) crystal system is also known as the isometric system. Cubic crystal system characterizes itself by its three equivalent crystallographic axes perpendicular to each other.
a = b = c
α = β = γ = 90°
primitive (cP)
body-centered (cI)
face-centered (cF)
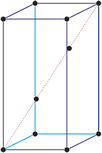
Hexagonal crystal system
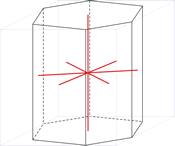
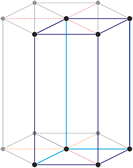
Hexagonal crystal system is based on four crystallographic axes. Three of the axes (denoted by a1, a2, and a3) are of the same length and lie in the hexagonal (basal) plane at 120° to one another (between the positive ends). A fourth axis (c), longer or shorter than other three, is perpendicular to this plane. Therefore, it is sufficient to give the a and c lattice parameters for the descriptioion of the hexagonal lattice.
The unit cell parameters are:
a = b ≠ c
α = β = 90° γ = 120°
The volume of the hexagonal unit cell is given by
primitive (hP)
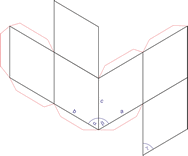
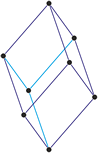
Trigonal crystal system
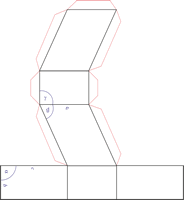
The trigonal crystal system is described by three primitive vectors of equal length that make equal angles (≠90°) with one another. The trigonal unit cell is like a cube that has been stretched along on body diagonal.
a = b = c
α = β = γ ≠ 90°
Referred to rhombohedral axes
Referred to hexagonal axes
primitive hexagonal lattice (hP)
primitive rhombohedral lattice (hR)
An alternative cell is sometimes used to describe the rhombohedral lattice. The cell is of the same shape as the conventional hexagonal unit cell with two interior points equally spaced along a diagonal. In practice, the hexagonal description is more commonly used because it is easier to deal with coordinate system with two 90° angles.
a = b ≠ c
α = γ = 90° β = 120°
R-centred hexagonal lattice (hR)
This figure shows the rhombohedrally-centred hexagonal cell and its relationship to the primitive rhombohedral cell
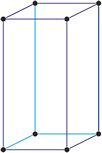
Tetragonal crystal system
Minerals of the tetragonal crystal system are referred to three mutually perpendicular axes. The two horizontal axes are of equal length, while the vertical axis is of different length and may be either shorter or longer than the other two.
a = b ≠ c
α = β = γ = 90°
primitive (tP)
body-centered (tI)
Orthorhombic crystal system
Minerals of the orthorhombic (or rhombic) crystal system are referred to three mutually perpendicular axes, each of which is of a different length than the others.
a ≠ b ≠ c
α = β = γ = 90°
primitive (oP)
base-centered (oC)
body-centered (oI)
face-centered (oF)
Monoclinic crystal system
Minerals of the monoclinic crystal system are referred to three unequal axes. Two of these axes (a and c) are inclined toward each other at an oblique angle; these are usually depicted vertically. The third axis (b) is perpendicular to the other two and is called the ortho axis. The two vertical axes therefore do not intersect one another at right angles, although both are perpendicular to the horizontal axis.
a ≠ b ≠ c
α = γ = 90° ≠ β
primitive (mP)
base-centered (mC)
Triclinic crystal system
Minerals of the triclinic crystal system are referred to three unequal axes, all of which intersect at oblique angles. The triclinic system is sometimes called the anorthic system because there are no angles that are orthogonal.
a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90°
primitive (aP)
Bibliography:
- International Tables for Crystallography. Volume A: Space-Group Symmetry. ed. Theo Hahn. Published for the International union of crystallography by Springer. Fifth edition, 2005.
- "Online Dictionary of Crystallography." 9 Dec. 2005. IUCr. 28 Apr. 2016. <http://reference.iucr.org/dictionary/Category:Fundamental_crystallography>.
- Cockcroft, Jeremy Karl and Barnes, Paul. "Powder Diffraction on the Web." 1 Feb. 2016. Birkbeck College, University of London. 4 July. 2016. <http://pd.chem.ucl.ac.uk/pd/welcome.htm>.
- Howard, Mike and Howard, Darcy. "Introducción a la Cristalografía y Sistemas Cristalinos." (Traducción al español: Juan José Palafox Reyes; colaborador Porfirio Sosa. Universidad de Sonora, México). Rockhounding Arkansas. 17 June 2016. <http://gaia.geologia.uson.mx/academicos/palafox/index.htm>.
- Infogalactic: the planetary knowledge core contributors. "Trigonal crystal system." 3 Sep. 2015. Infogalactic: the planetary knowledge core. 5 Nov. 2019. <https://infogalactic.com/info/Trigonal_crystal_system>.
Citing this page:
Generalic, Eni. "Crystal systems and Bravais lattices." EniG. Periodic Table of the Elements. KTF-Split, 18 Jan. 2024. Web. {Date of access}. <https://www.periodni.com/crystal-systems-and-bravais-lattices.html>.
